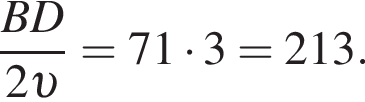Одно число меньше другого на 64, что составляет 16% большего числа. Найдите меньшее число.
На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 102°, ∠BOM = 128°. Найдите величину угла BOC.
Длины катетов прямоугольного треугольника являются корнями уравнения x2 − 9x + 6 = 0. Найдите площадь треугольника.
Вычислите 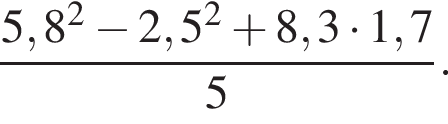
Упростите выражение
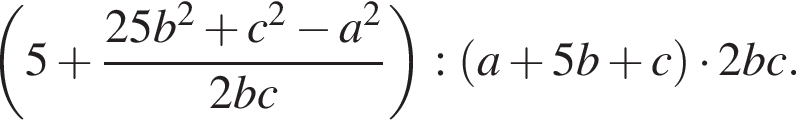
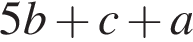
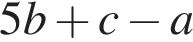
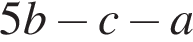
Корень уравнения
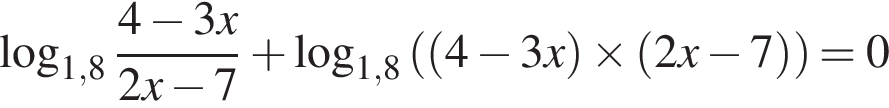
(или сумма корней, если их несколько) принадлежит промежутку:
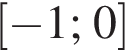
Найдите длину средней линии прямоугольной трапеции с острым углом 60°, у которой большая боковая сторона и большее основание равны 6.
Секущая плоскость пересекает сферу по окружности, радиус которой равен 3. Если расстояние от центра сферы до секущей плоскости равно 6, то площадь сферы равна:
Укажите номера пар неравенств, которые являются равносильными.
1) (x − 14)2 < 0 и x − x2 − 14 ≥ 0;
2) x2 − 169 > 0 и |x| < 13;
3) x2 + x − 30 < 0 и (x − 5)(x + 6) < 0;
4) x2 ≥ 31 и 
5) 5x2 < 9x и 5x < 9.
Найдите количество всех целых решений неравенства 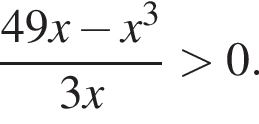
Точки А(2;3), B(7;5) и C(10;5) — вершины трапеции ABCD (AD||BC). Найдите сумму координат точки D, если 
Найдите произведение корней уравнения 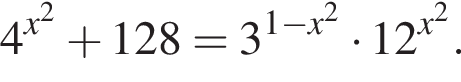
Найдите
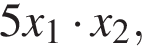 где
где ![]() — абсциссы точек пересечения параболы и горизонтальной прямой (см.рис.).
— абсциссы точек пересечения параболы и горизонтальной прямой (см.рис.).
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Найдите количество корней уравнения  на промежутке
на промежутке 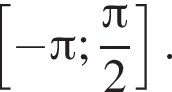
Выберите три верных утверждения, если известно, что  и
и 
1) ![]() — угол первой четверти
— угол первой четверти
2) 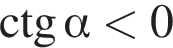
3) 
4) 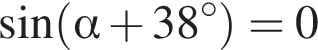
5) 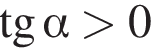
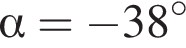
6) 
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 234.
Выберите три верных утверждения:
1) если 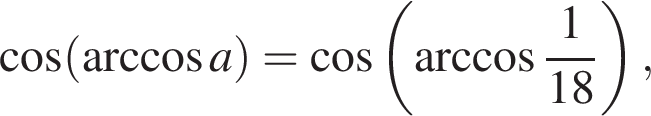 то
то 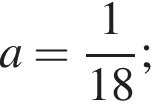
2) если 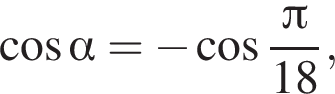 то
то 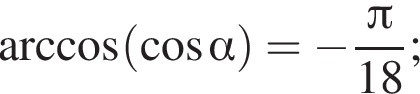
3) если 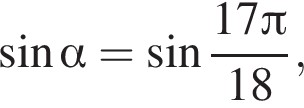 то
то 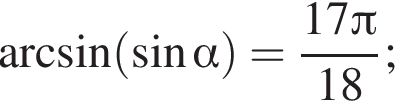
4) если 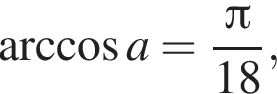 то
то 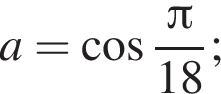
5) если 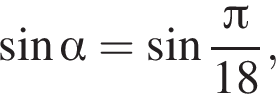 то
то 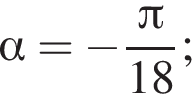
6) если 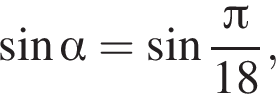 то
то 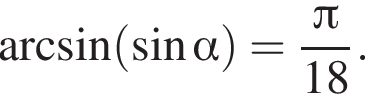
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Пусть (x; y) — решение системы уравнений 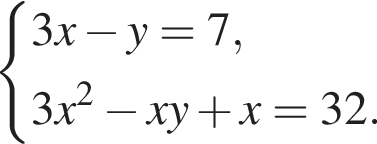
Найдите значение 3y − x.
Найдите увеличенное в 16 раз произведение абсцисс точек пересечения прямой y = 6 и графика нечетной функции, которая определена на множестве  и при x > 0 задается формулой
и при x > 0 задается формулой 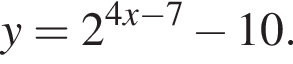
Дана арифметическая прогрессия −24; −20; −16; ... . Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Разность этой прогрессии равна ...
Б) Четвертый член этой прогрессии равен ...
В) Сумма шести первых членов этой прогрессии равна ...
1) −84
2) −80
3) 0
4) 4
5) −12
6) −4
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Найдите сумму целых значений x, принадлежащих области определения функции
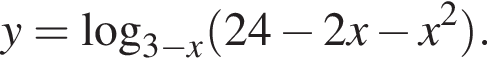
Найдите произведение наибольшего целого отрицательного и наибольшего целого положительного решений неравенства 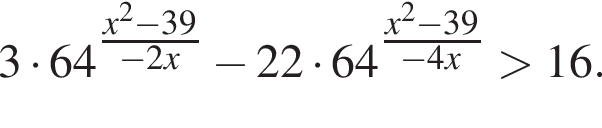
Найдите сумму целых решений неравенства 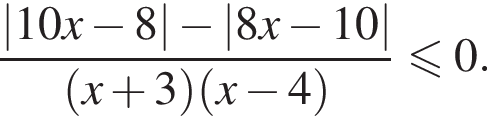
Пусть 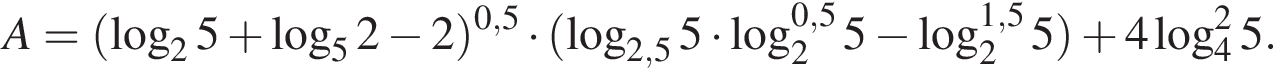
Найдите значение выражения 2A.
Через электронный сервис Маша купила билет на концерт и заплатила 80 руб. В эту сумму входит стоимость билета и сервисный сбор 4 руб. За неделю до концерта Маша-решила вернуть билет. По правилам организатора концерта ей вернут не менее 75% стоимости билета. Какую наибольшую сумму (в рублях) может потерять Маша, вернув билет?
Найдите произведение наименьшего целого решения на количество всех натуральных решений системы неравенств
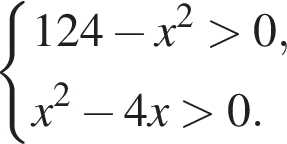
Найдите все пары (m, n) целых чисел, которые связаны соотношением m2 + 4m = n2 − 2n + 8. Пусть k — количество таких пар, m0 — наименьшее из значений m, тогда значение выражения k · m0 равно ... .
ABCDA1B1C1D1 — прямая четырехугольная призма, объем которой равен 720. Основанием призмы является параллелограмм ABCD. Точки M и N принадлежат ребрам A1D1 и С1D1, так что A1M : MD1 = 1 : 2, D1N : NC1 = 1 : 2. Отрезки A1N и B1M пересекаются в точке K. Найдите объем пирамиды SB1KNC1, если  и B1S : SD = 3 : 1.
и B1S : SD = 3 : 1.
Отрезок BD является биссектрисой треугольника АВС, в котором 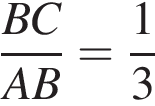 и
и 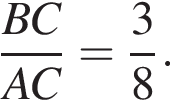 По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 11 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 11 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?

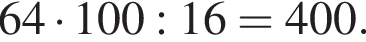 Таким образом, меньшее число
Таким образом, меньшее число 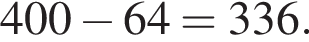
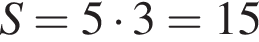 см2.
см2.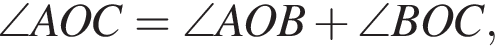
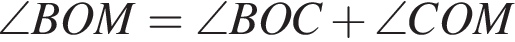 и
и  Таким образом:
Таким образом:
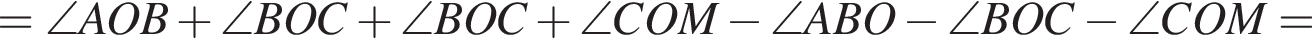
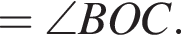
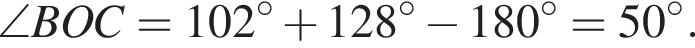
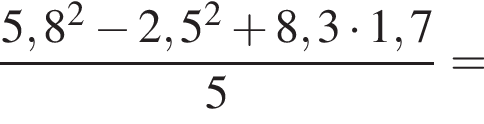
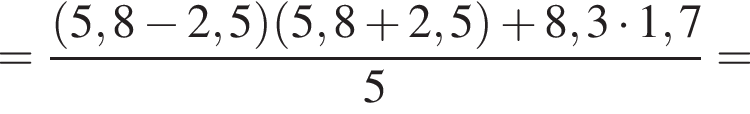
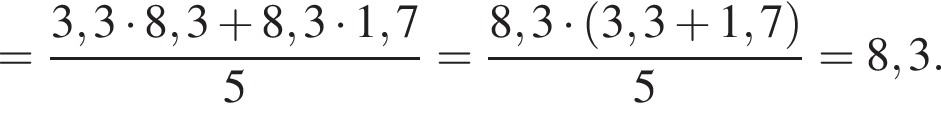
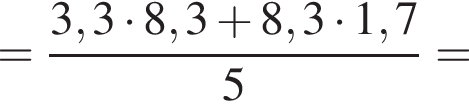
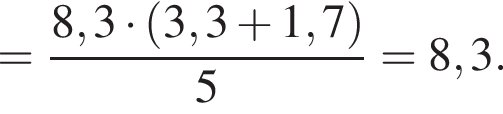
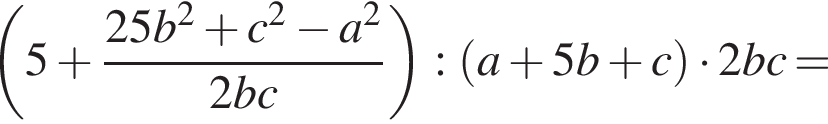
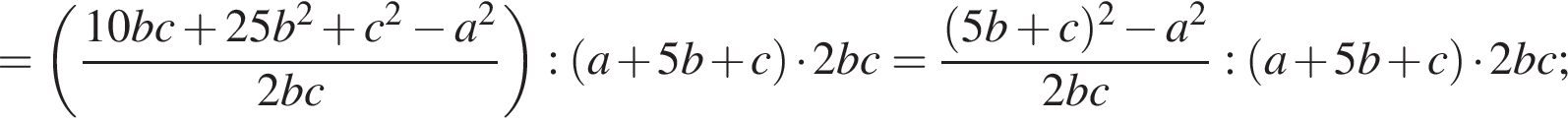
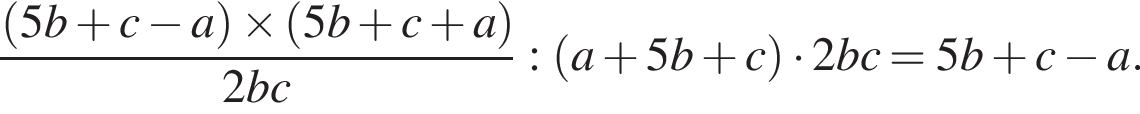
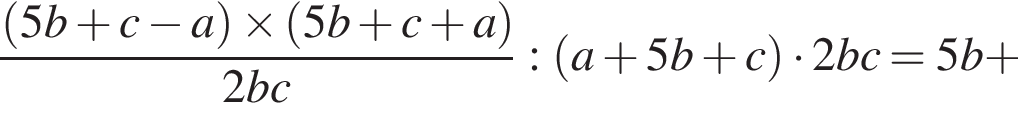
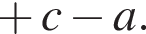
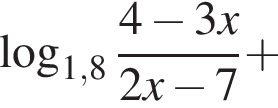
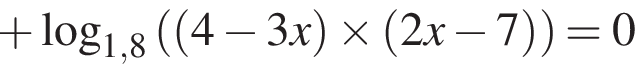
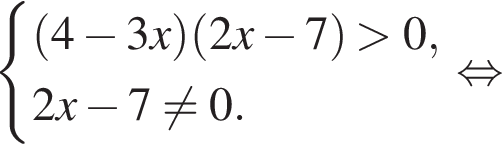
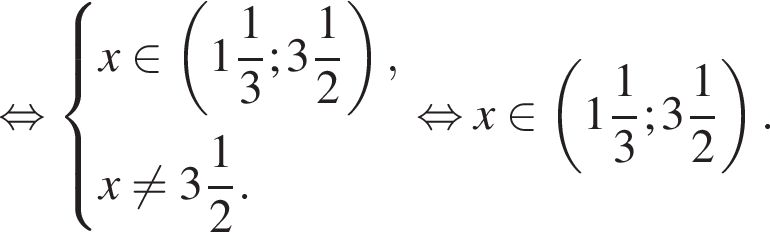
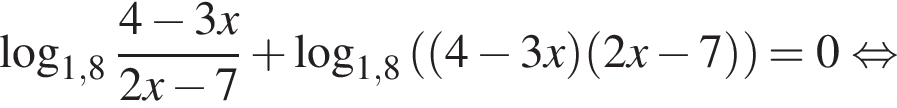
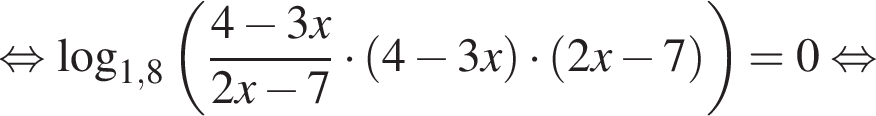
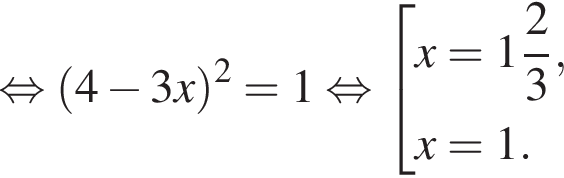
 поэтому
поэтому 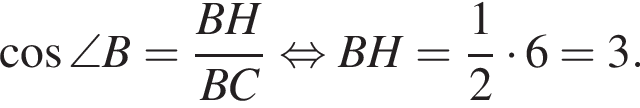 Следовательно,
Следовательно, 
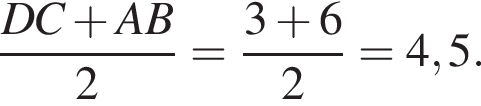
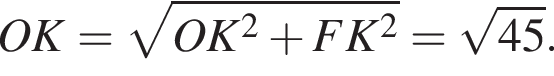 Таким образом, OK = R =
Таким образом, OK = R = 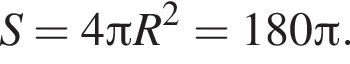
 решением второго неравенства является интервал
решением второго неравенства является интервал 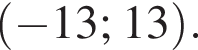 Таким образом, неравенства неравносильны.
Таким образом, неравенства неравносильны.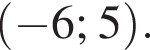 Неравенства равносильны.
Неравенства равносильны. а решением второго — полуинтервал
а решением второго — полуинтервал 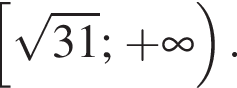
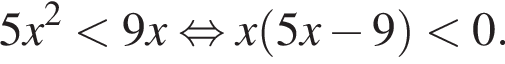 Неравенства неравносильны, так как первое неравенство имеет большее количество нулей.
Неравенства неравносильны, так как первое неравенство имеет большее количество нулей.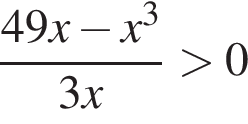
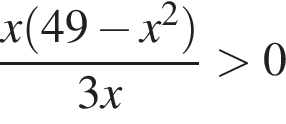
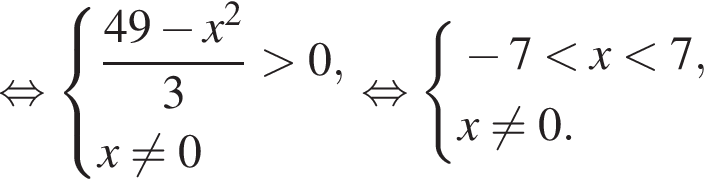
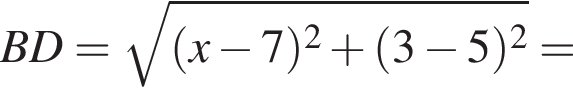
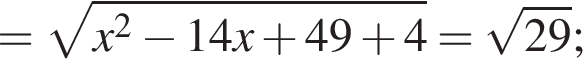
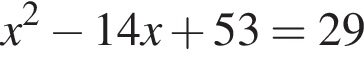
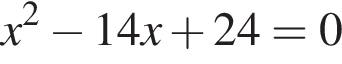
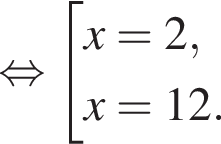
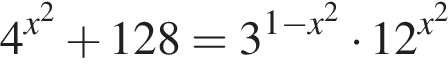
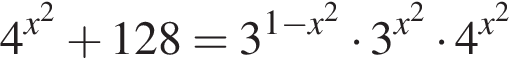
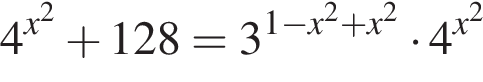
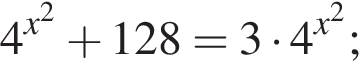
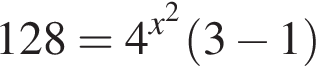
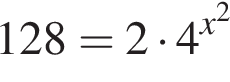
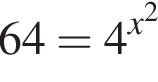
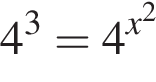
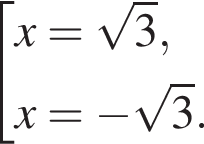
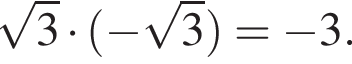
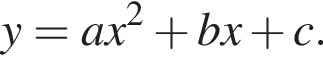 На рисунке изображена парабола с ветвями, направленными вниз, следовательно,
На рисунке изображена парабола с ветвями, направленными вниз, следовательно, 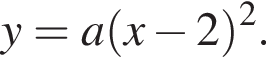 Для того, чтобы найти a, подставим в уравнение параболы точку (1;-1), через которую данная парабола проходит:
Для того, чтобы найти a, подставим в уравнение параболы точку (1;-1), через которую данная парабола проходит: 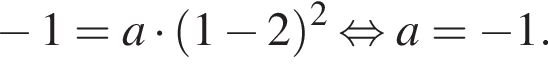 Таким образом, изображённая на графике парабола задается уравнением
Таким образом, изображённая на графике парабола задается уравнением 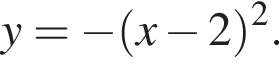
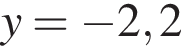 :
: 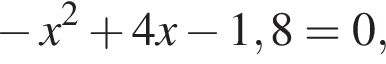 откуда по теореме Виета
откуда по теореме Виета 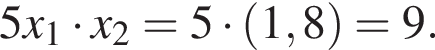
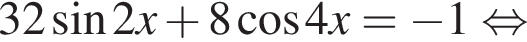
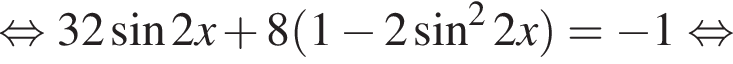
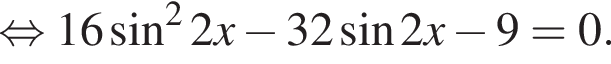
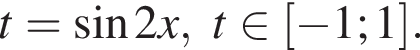 Тогда:
Тогда: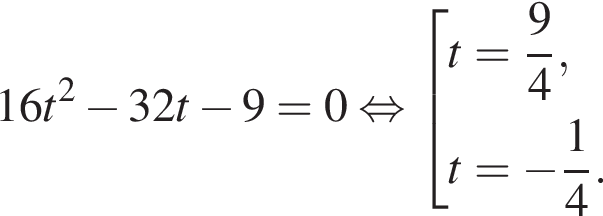
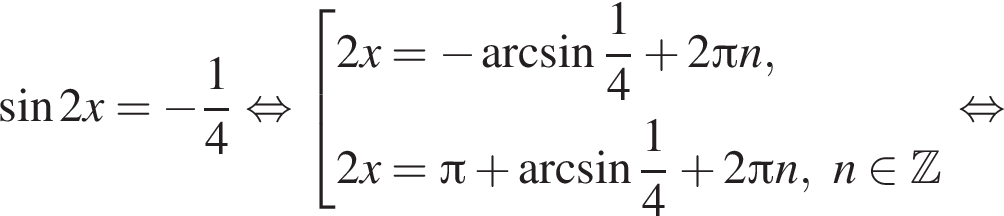
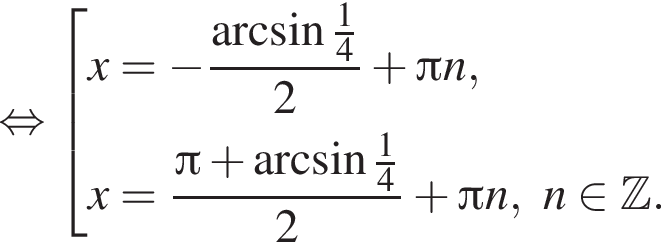
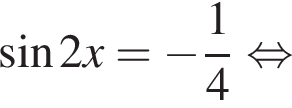
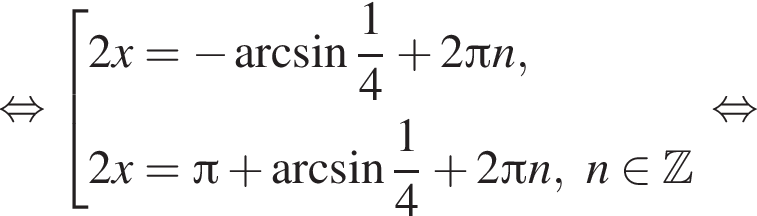
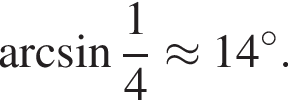 Рассмотрим значения x при различных значениях n:
Рассмотрим значения x при различных значениях n: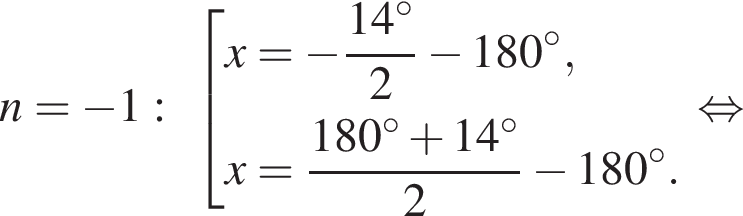
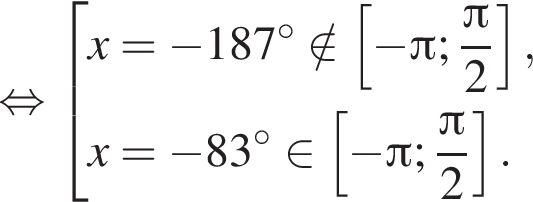

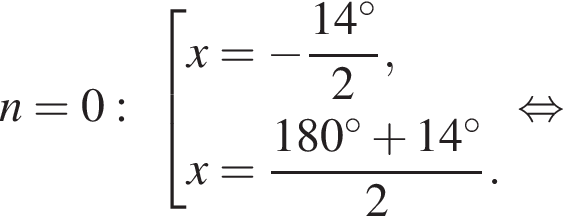
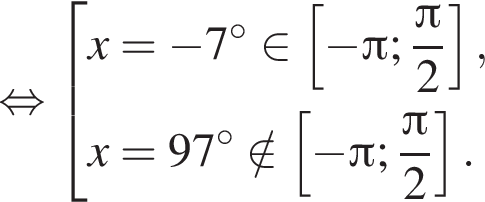
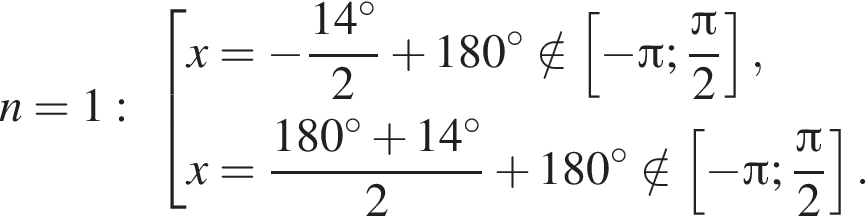
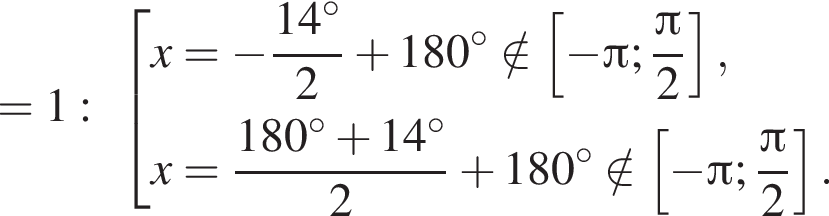
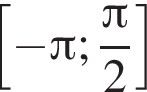 2 корня.
2 корня.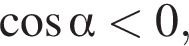 а
а 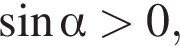 то
то 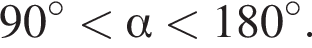 Заметим, что
Заметим, что 
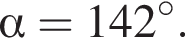 Тогда
Тогда 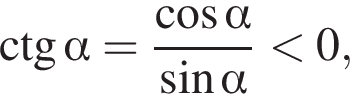 так как
так как 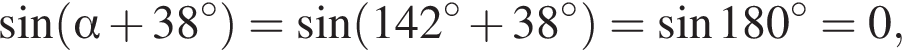
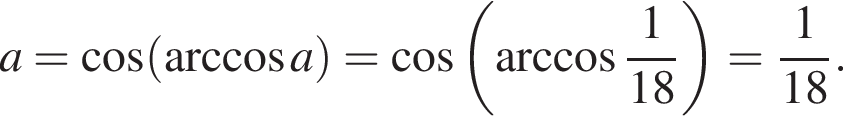

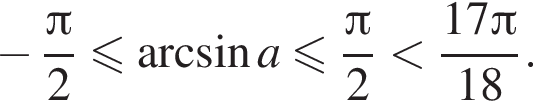
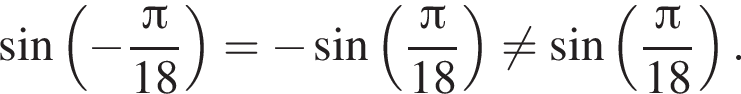

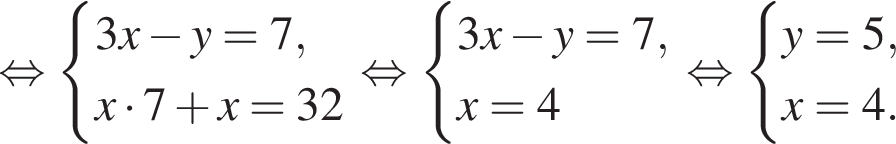
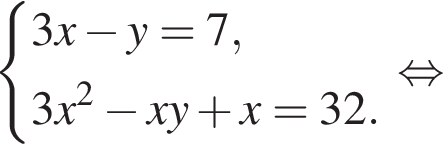
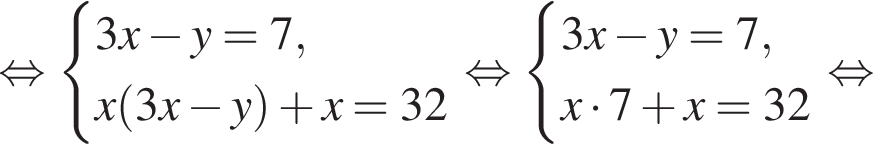
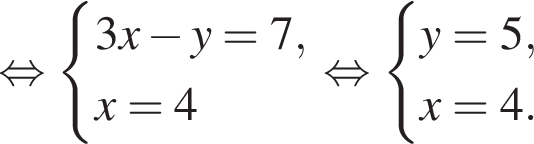
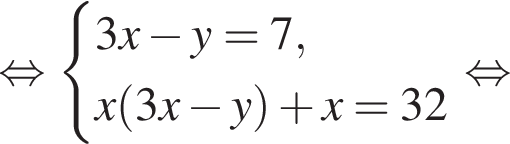
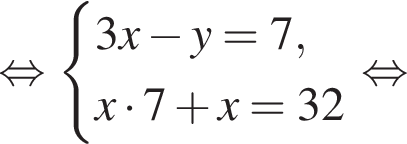

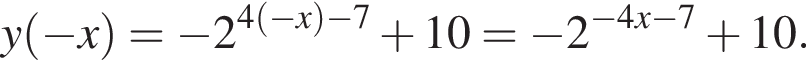
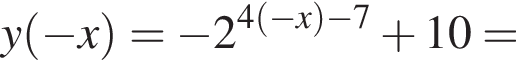
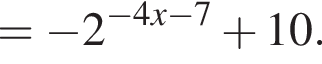
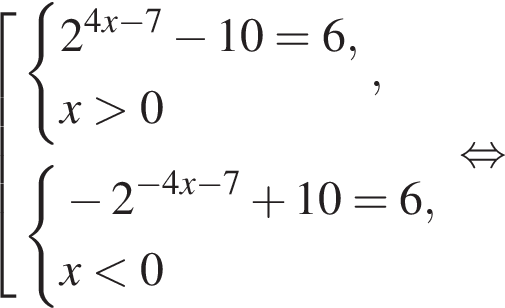
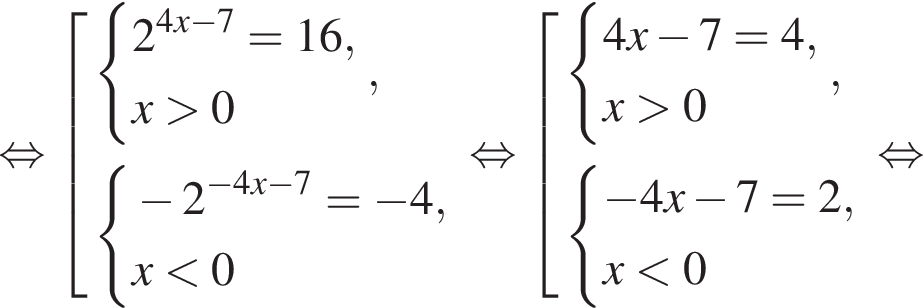
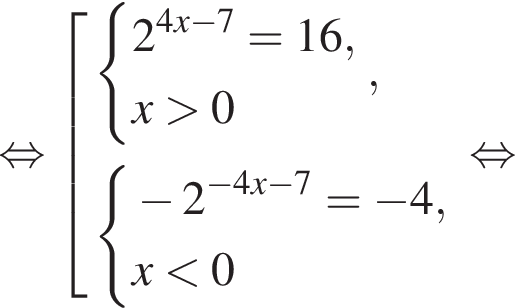
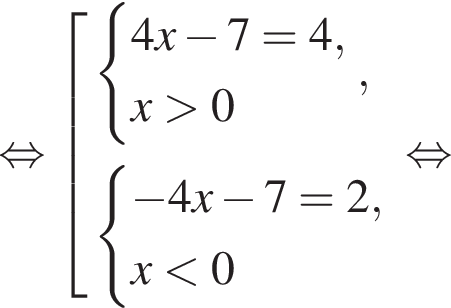
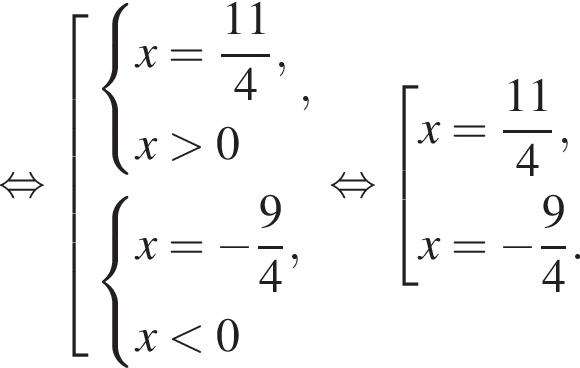
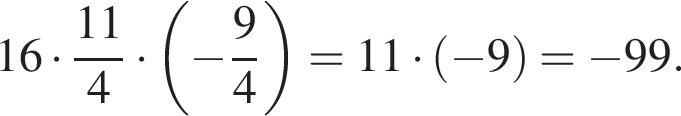
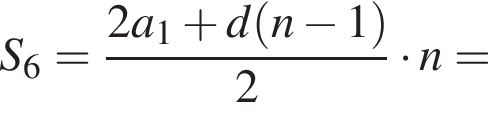
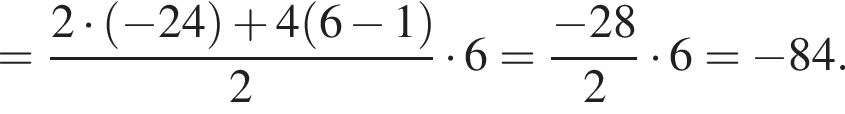
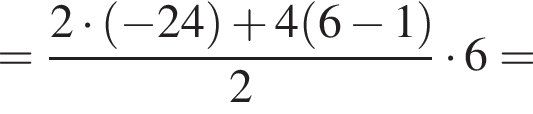
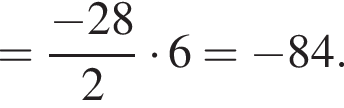
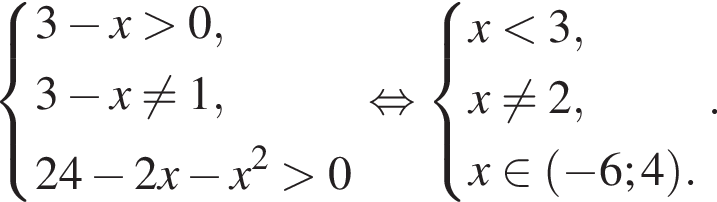
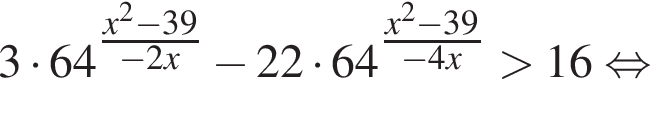
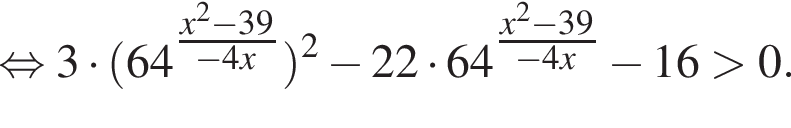
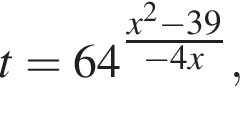 тогда имеем:
тогда имеем: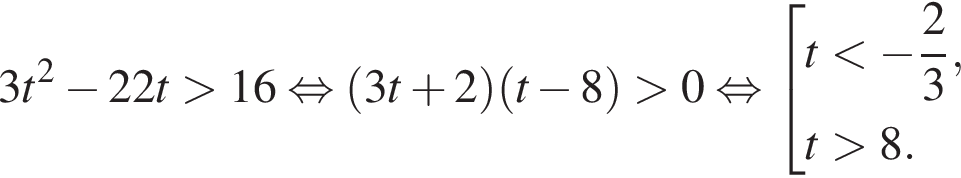
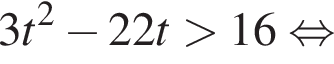
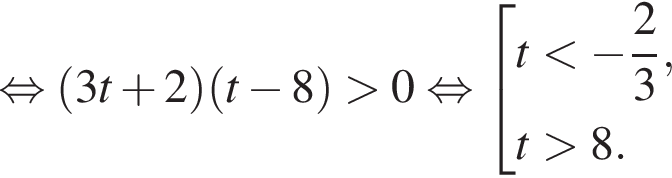
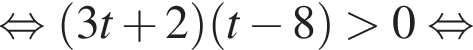
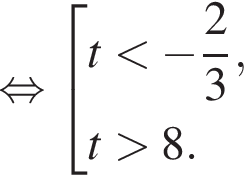
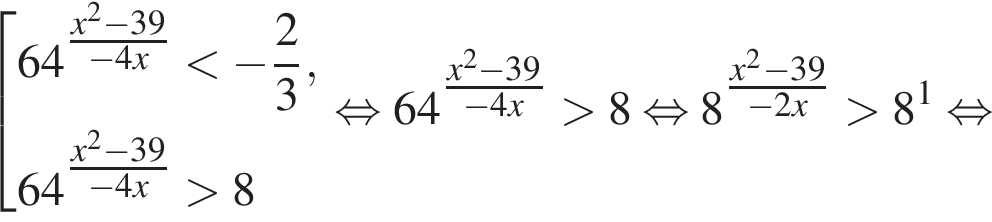
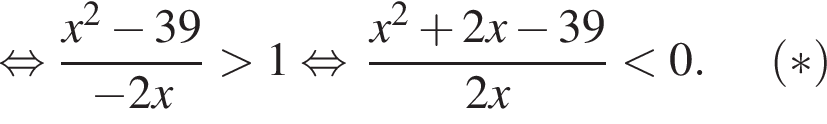
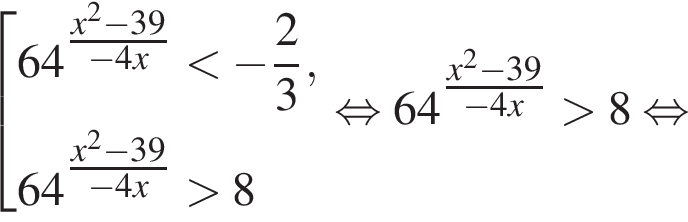
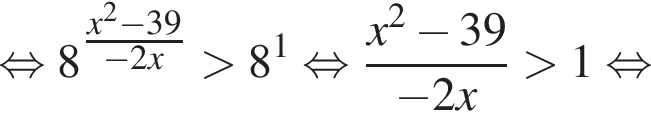
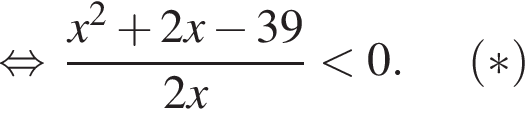
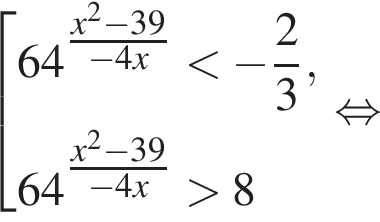
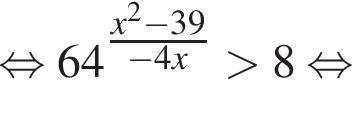
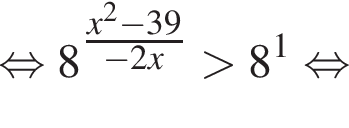
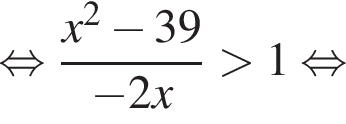
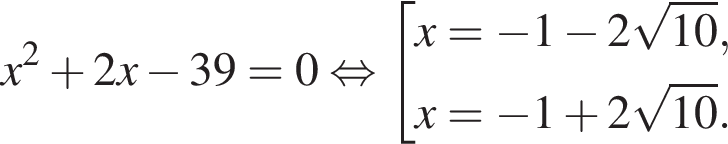
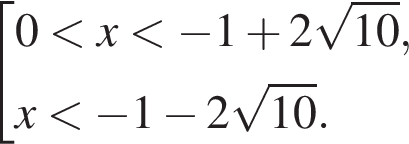
 совпадает со знаком разности
совпадает со знаком разности  имеем:
имеем: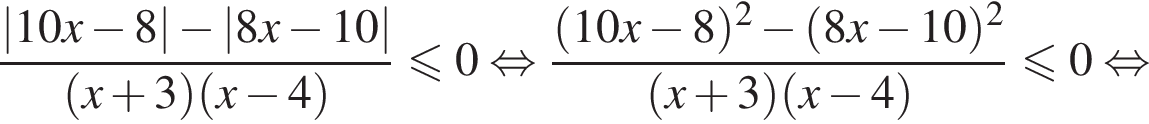
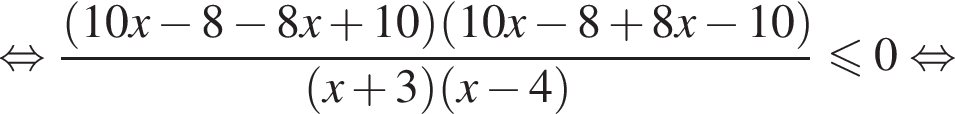
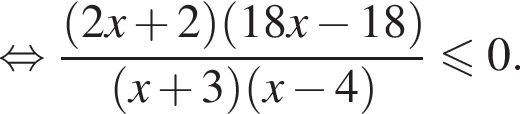
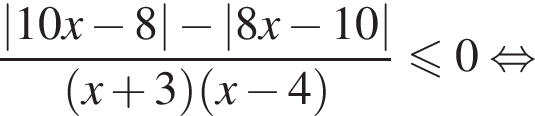
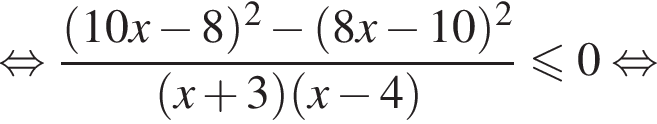
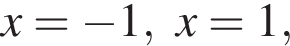 корни знаменателя
корни знаменателя 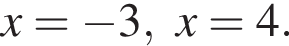 Поэтому:
Поэтому: 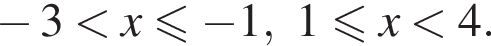 Целые решения — числа −2, -1, 1, 2, 3. Их сумма равна 3.
Целые решения — числа −2, -1, 1, 2, 3. Их сумма равна 3.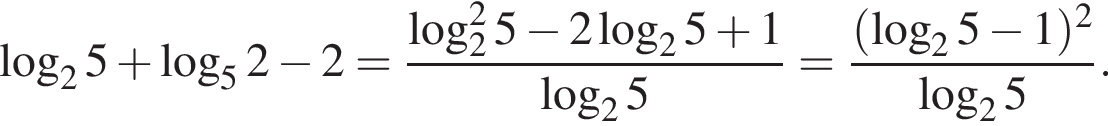
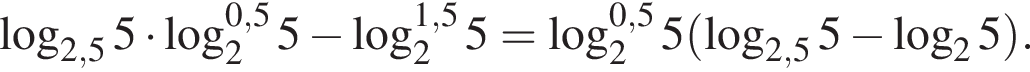
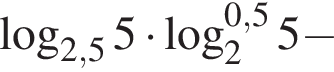
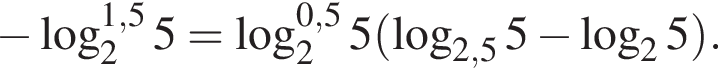
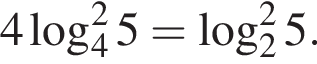 Тогда имеем:
Тогда имеем: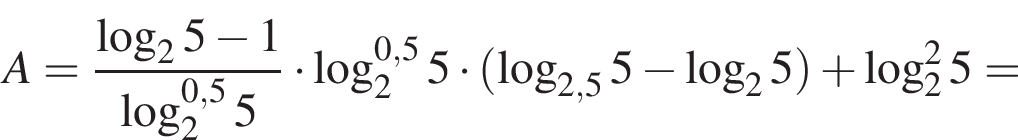
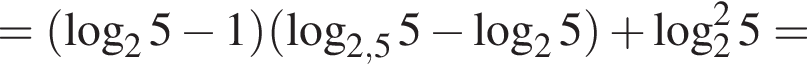
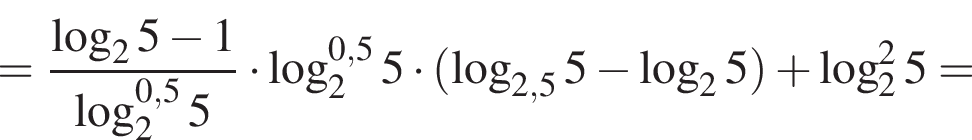
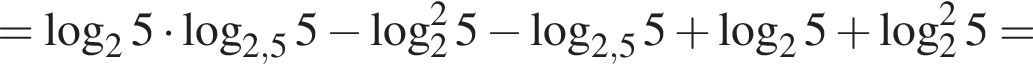
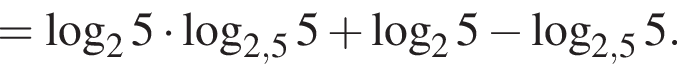
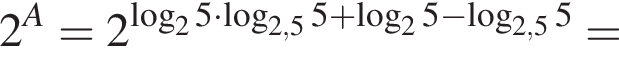
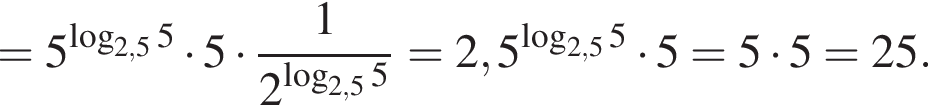
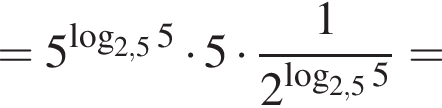
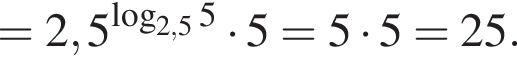
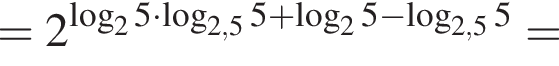
 Деньги, уплаченные за сервисный сбор, Маше не вернут, таким образом, наибольшая сумма, которую Маша может потерять, вернув билет, равна 23 руб.
Деньги, уплаченные за сервисный сбор, Маше не вернут, таким образом, наибольшая сумма, которую Маша может потерять, вернув билет, равна 23 руб.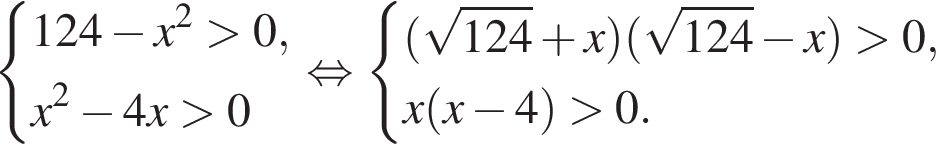
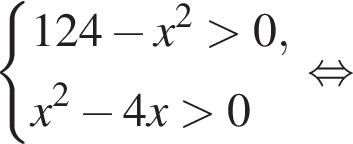
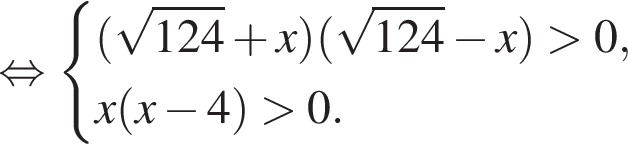
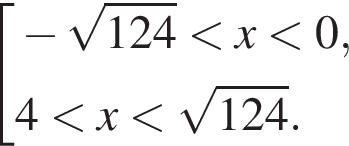
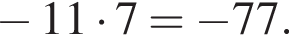
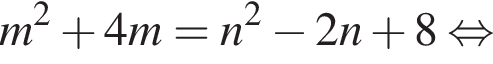
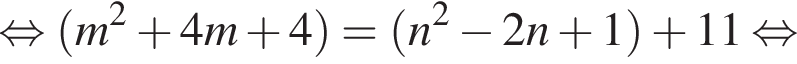
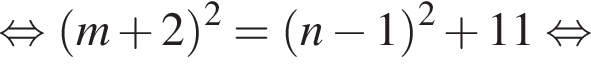
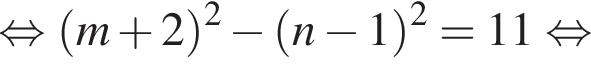
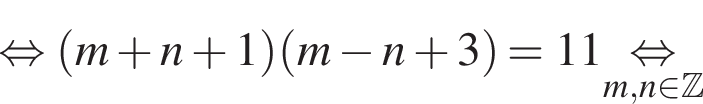
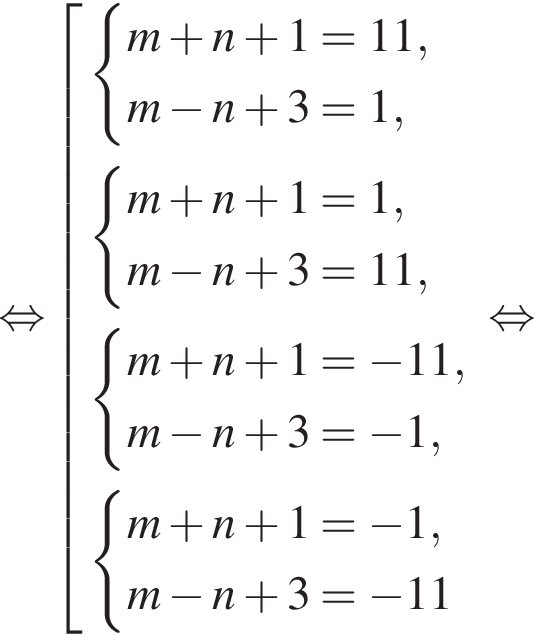
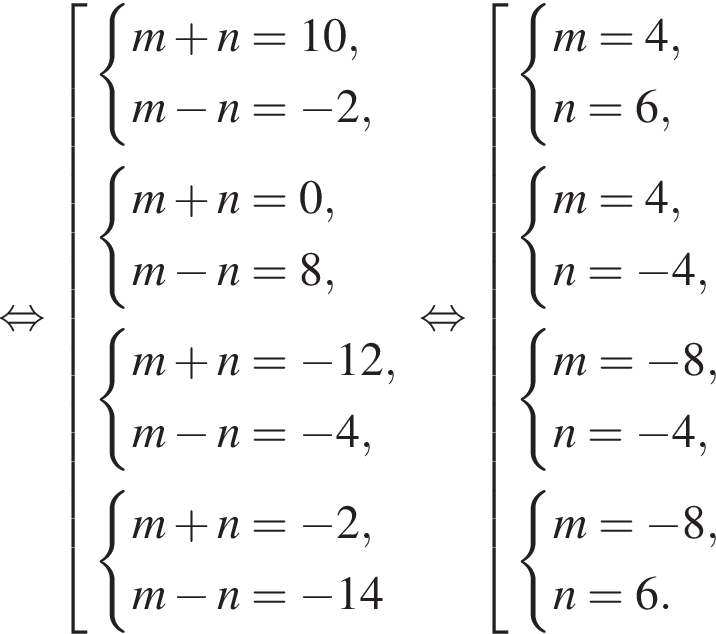
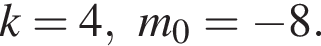 Получаем
Получаем 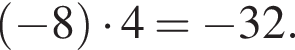
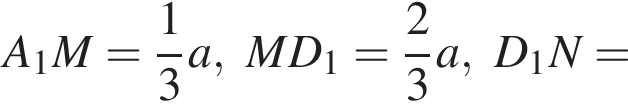
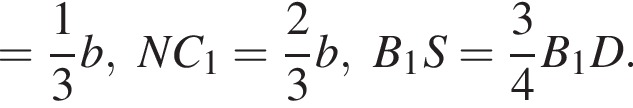
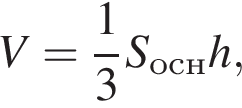 где основание — KNC1B1. Проведем высоту SE из точки S пирамиды SB1KNC1, как показано на рисунке.
где основание — KNC1B1. Проведем высоту SE из точки S пирамиды SB1KNC1, как показано на рисунке.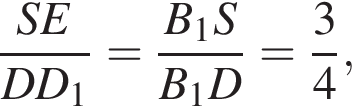 поэтому
поэтому 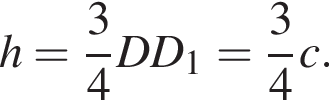

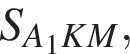 для этого сделаем дополнительное построение, проведя прямую параллельную B1M до пересечения с продолжением стороны A1D1. Получившийся треугольник D1NF подобен треугольнику A1B1M по двум углам. Поэтому:
для этого сделаем дополнительное построение, проведя прямую параллельную B1M до пересечения с продолжением стороны A1D1. Получившийся треугольник D1NF подобен треугольнику A1B1M по двум углам. Поэтому: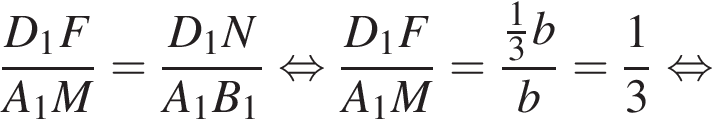
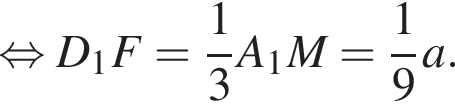

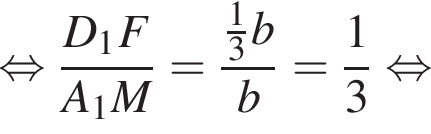
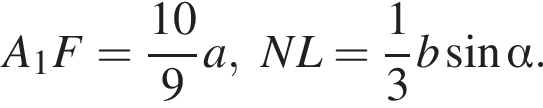 Соответственно, площадь треугольника A1NF равна
Соответственно, площадь треугольника A1NF равна 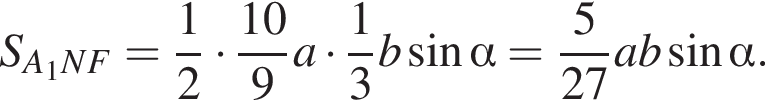 Треугольники A1KM и A1NF подобны с коэффициентом подобия:
Треугольники A1KM и A1NF подобны с коэффициентом подобия: 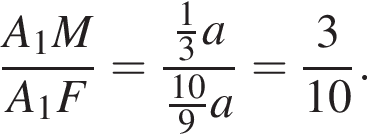 Отсюда площадь треугольника A1KM равна
Отсюда площадь треугольника A1KM равна 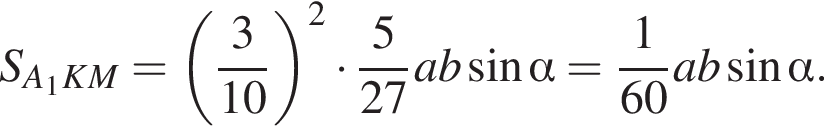

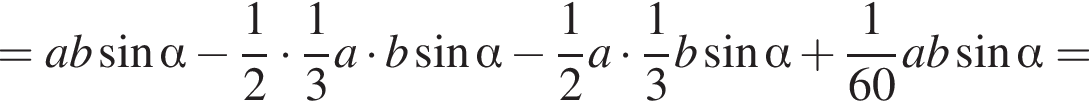
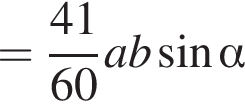
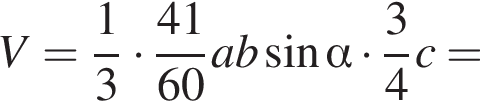
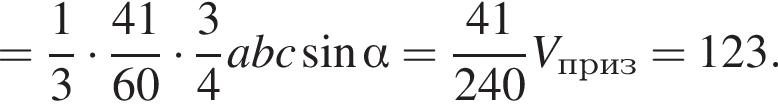
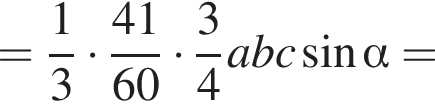
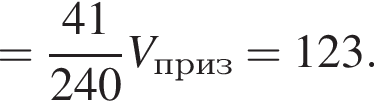
 По свойству биссектрисы получаем, что
По свойству биссектрисы получаем, что 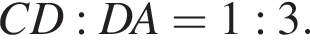 Значит, если
Значит, если  то
то 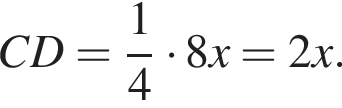
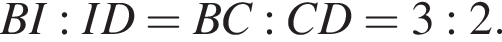 Значит, можно считать, что скорость первого тела равна 3υ, а второго 2υ. Время движения обратно пропорционально скорости, из условия следует, что
Значит, можно считать, что скорость первого тела равна 3υ, а второго 2υ. Время движения обратно пропорционально скорости, из условия следует, что 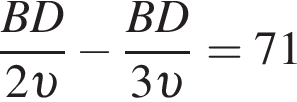
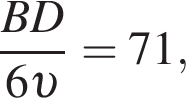 откуда
откуда